Самостійна робота С-9 [18М] Варіант 3

(Сторінка 45)

1. На якому з малюнків зображено коло, вписане у трикутник?
   

А.
Б.✅
В.
Г.

2. Накресліть коло радіусом 24 мм. Проведіть у ньому діаметр MN та хорду AK. За допомогою косинця проведіть дотичну до кола, що проходить через точку M.

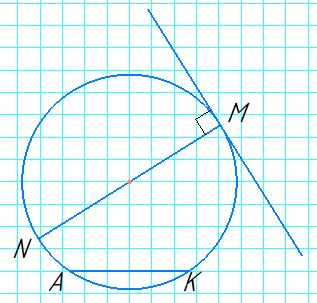
3. На малюнку точко O — центр кола, ∠AOL = 78°. Знайдіть ∠AKL.
   
   

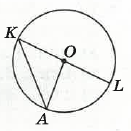
OA = OK (як радіуси), тому ∆KOA – рівнобедрений.

∠AOL – зовнішній кут ∆KOA. Згідно теореми ∠AOL = ∠OKA + ∠OAK.

Так як ∠OKA = ∠OAK, то ∠AOL = 2∠OKA ⇒ ∠OKA = ∠AOL : 2 = 78° : 2 = 39°.

∠AKL = ∠OKA = 39°.

4. Прямі BK i BL дотикаються до кола із центром O в точках K i L, ∠KBL = 60°. Знайдіть довжину BO, якщо радіус кола дорівнює 8 см.

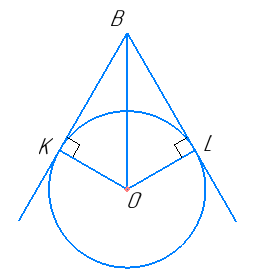
KB⟂ОK і BL⟂ОL (за властивістю дотичних). ∆BKO і ∆BLO – прямокутні.

ОK = ОL (як радіуси), ОB – спільна, отже ∆BOK = ∆BOL за гіпотенузою і катетом. У рівних трикутників усі відповідні елементи рівні, тому ∠OBL = ∠OBK = $\frac{1}{2}$ ∠KBL = $\frac{1}{2}$ ⋅ 60° = 30°.

Оскільки в прямокутному трикутнику катет, що лежить навпроти кута 30° дорівнює половині гіпотенузи, то:

ОВ = 2 ⋅ LO = 2 ⋅ 8 = 16 см.