Самостійна робота С-8 [16М] Варіант 3
(Сторінка 39)
- Знайдіть другий гострий кут прямокутного трикутника, якщо перший дорівнює 34°.
А. 66°
Б. 56°✅
В. 34°
Г. 46°
-
На малюнку MT ⊥ CD, CM = MD. Доведіть що ∆CMT = ∆DMT.
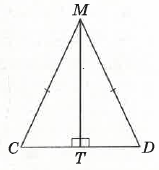
У ∆CMT і ∆DMT:
MT спільна для обох трикутників
CM = MD (дано)
∠CMT = ∠DMT = 90° (оскільки MT ⊥ CD)
∆CMT і ∆DMT – прямокутні
Отже, ∆CMT = ∆DMT згідно теореми (ознаки рівності прямокутних трикутників за катетом і гіпотенузою).
-
Периметр трикутника дорівнює 24 дм. Чи може одна з його сторін дорівнювати:
Згідно теореми про нерівність трикутника, кожна сторона трикутника має бути менша від суми двох інших його сторін. Отже:
1) 24 – 11 = 13 (дм) – сума двох інших сторін
За нерівністю трикутника: 11 < 13 – умова виконується, така сторона можлива.
2) 24 – 12 = 12 (дм) – сума двох інших сторін
За нерівністю трикутника: 12 = 12 – умова не виконується, така сторона неможлива для трикутника.
3) 24 – 13 = 11 (дм) – сума двох інших сторін
За нерівністю трикутника: 13 > 11 – умова не виконується, така сторона неможлива.
-
У прямокутному трикутнику один з гострих кутів на 30° більший за другий, а сума гіпотенузи й меншого катета дорівнює 18 см. Знайдіть гіпотенузу трикутника.
Позначимо гострі кути трикутника як α та α + 30°. Оскільки сума гострих кутів прямокутного трикутника дорівнює 90°, маємо:
α + (α + 30°) = 90°
2α + 30° = 90°
2α = 60°
α = 30° - менший гострий кут
α + 30° = 60° - більший гострий кут
У трикутнику з кутами 30° і 60° відомо, що менший катет дорівнює половині гіпотенузи. Позначимо гіпотенузу трикутника як х, тоді катет $\frac{х}{2}$.
За умовою, сума гіпотенузи й меншого катета дорівнює 18 см:
х + $\frac{х}{2}$ = 18
$\frac{3х}{2}$ = 18
3х = 36
х = 12
Відповідь: 12 см.
