Діагностична (контрольна) робота ДР-5 [10М] Варіант 3

(Сторінка 50)

1. Знайдіть радіус кола, діаметр якого дорівнює 16 см

А. 4 см
Б. 32 см
В. 16 см
Г. 8 см✅

2. Знайдіть градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює 60°

А. 30°✅
Б. 60°
В. 15°
Г. 120°

3. На якому з малюнків зображено коло, описане навколо трикутника?
   
   

А.
Б.
В.✅
Г.

4. Точка O — центр кола, CD — його хорда. Знайдіть ∠OCD, якщо ∠COD = 88°
   
   

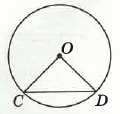
Радіус ОC = OD, отже трикутник ОCD – рівнобедрений.
∠OCD = ∠ODC (як кути при основі рівнобедреного трикутника)
∠COD + ∠OCD + ∠ODC = 180°
88° + 2 ⋅ ∠OCD = 180°
2 ⋅ ∠OCD = 180° – 88°
2 ⋅ ∠OCD = 92°
∠OCD = 92° : 2
∠OCD = 46°

5. Кола, радіуси яких дорівнюють 8 см і 3 см, мають внутрішній дотик. Знайдіть відстань між центрами кіл.

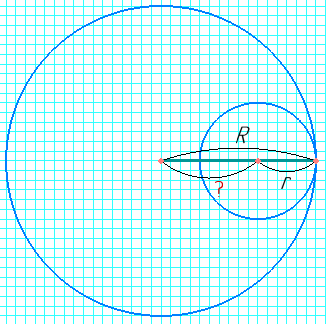
Для кіл з внутрішнім дотиком відстань між центрами дорівнює різниці радіусів:
d = R – r = 8 – 3 = 5 см

6. Накресліть відрізок KA, довжина якого 5 см. За допомогою лінійки з поділками і косинця проведіть серединний перпендикуляр до відрізка KA.

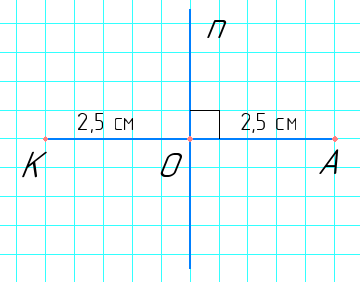
Пряма n ⊥ КА.
КO = OА = 2,5 см.

7. Два кола мають зовнішній дотик. Знайдіть радіуси цих кіл, якщо один з них у 4 разів більший за другий а відстань між їхніми центрами дорівнює 15 см.

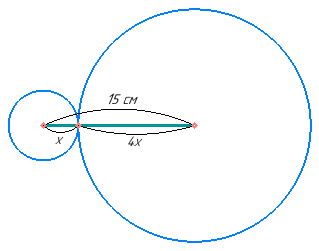
Нехай радіус меншого кола дорівнює x, тоді більшого – 4x:
4x + x = 15
5x = 15
x = 3 (см) – радіус меншого кола
4x = 4 ⋅ 3 = 12 (см) – радіус більшого кола

8. Побудуйте рівнобедрений трикутник, основа якого дорівнює відрізку с, а кут при основі — куту N.
   
   

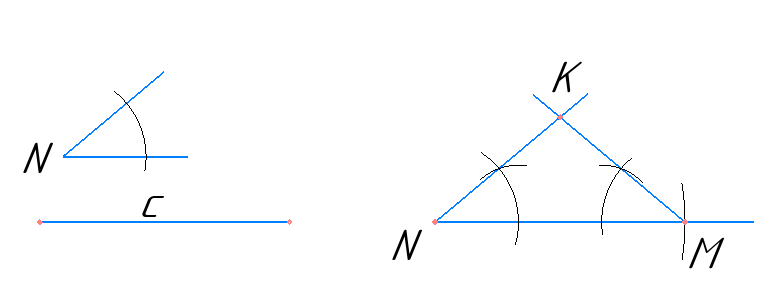
План побудови:
1) Будуємо промінь. Відкладаємо на ньому відрізок NM = c;
2) Будуємо кут ∠N та ∠М = ∠N;
3) Продовжуємо промені побудованих кутів до перетину в точці K;
4) ∆MNK – шуканий рівнобедрений трикутник.

9. Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 2 см і 7 см, починаючи від основи. Знайдіть периметр трикутника.

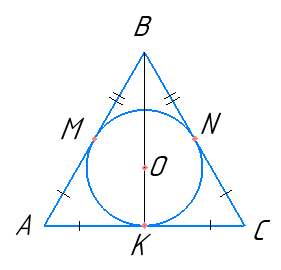
Нехай ABC заданий рівнобедрений трикутник. AB = BC. M, N, K – точки дотику вписаного кола до сторін трикутника ABC. BM = 7 см, AM = 2 см.
За властивістю дотичних:
BN = BM = 7 см;
AM = AK = CN = CK = 2 см;
Тоді, P_∆ABC = 2(AM + MB + AK) = 2(2 + 7 + 2) = 2  ⋅ 11 = 22 см.