Діагностична (контрольна) робота ДР-4 [8М] Варіант 2

(Сторінка 41)

1. Три кути трикутника можуть дорівнювати...
   

А. 70°; 60°; 50°✅
Б. 50°; 30°; 10°
В. 40°; 50°; 100°
Г. 40°; 40°; 90°

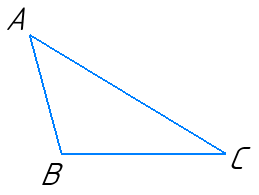
2. У ∆ABC ∠A < ∠B. Порівняйте між собою AC i BC цього трикутника.

У трикутнику проти більшого кута лежить більша сторона.

А. Порівняти не можливо
Б. AC < BC
В. AC = BC
Г. AC > BC✅

3. З’ясуйте, за якими елементами прямокутні трикутники, зображені на малюнку, рівні між собою?
   
   

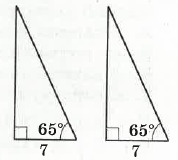
А. за катетом і гіпотенузою
Б. за катетом і прилеглим гострим кутом✅
В. за катетом і протилежним гострим кутом
Г. за гіпотенузою і гострим кутом

4. Кут при вершині рівнобедреного трикутника дорівнює 40°. Знайдіть кути при його основі.

У рівнобедреного трикутника кути при основі рівні, тому:
180° - 40° = 140° - сума кутів при основі
140° : 2 = 70° - кут при основі

5. На малюнку KM — висота ∆AKP. Знайдіть кути цього трикутника.
   
   

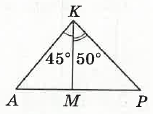
∠AKP = 45° + 50° = 95°
∠KAM = 180° - 45° - 90° = 45°
∠KPM = 180° - 50° - 90° = 40°

6. Дві сторони трикутника дорівнюють 5,2 см і 7,5 см. Якому найменшому числу сантиметрів може дорівнювати третя сторона?

Згідно теореми про нерівність трикутника, кожна сторона трикутника має бути менша від суми двох інших його сторін.
7,5 – 5,2 = 2,3 см
5,2 + 7, 5 = 12,7 см
Довжина третьої сторони повинна бути більшою за 2,3 см і меншою за 12,7 см.
Найменше ціле число, яке задовольняє цю умову, — 3 см.

7. Один з кутів трикутника вдвічі менший від другого й на 8° більший за третій. Знайдіть кути трикутника.

Нехай кути дорівнюють x, 2x, x - 8°
x + 2x + x - 8° = 180°
4x = 172°
x = 43° - перший кут
2x = 2 ⋅ 43° = 86° - другий кут
x - 8° = 43° – 8° = 35° - третій кут

8. Один із зовнішніх кутів трикутника дорівнює 108°. Знайдіть внутрішні кути, не суміжні з ним, якщо вони відносяться як 5 : 7.

Нехай кути дорівнюють 5x, 7x
Оскільки, суміжний кут дорівнює сумі двох інших кутів трикутника не суміжних з ним, то:
5x + 7x = 108°
12x = 108°
x = 9°
5x = 5 ⋅ 9° = 45° - один кут
7x = 7 ⋅ 9° = 63° - другий кут

9. У ∆ABC ∠C = 90°, ∠BAC = 60°, AT — бісектриса трикутника. Знайдіть довжину катета CB, якщо TB = 12 см.

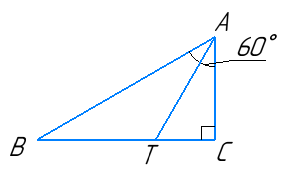
∆BCA – прямокутний, тоді ∠B = 90° - 60° = 30°.
Оскільки AT – бісектриса, то ∠TAC = ∠TAB = 30°.
Оскільки ∠TAB = ∠TBA, то ∆BAT - рівнобедрений з основою BA
AT = BT = 12 см
TC = AT : 2 = 12 : 2 = 6 см (згідно властивості катета, що лежить проти кута 30°)
CB = CT + BT = 6 + 12 = 18 см
Відповідь: 18 см.