Діагностична (контрольна) робота ДР-3 [6М] Варіант 3

(Сторінка 34)

1. ∆ABC — різносторонній, ∠BAM = ∠CAM. Тоді відрізок AM є ... трикутника
   
   

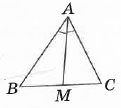
А. Висотою
Б. Бісектрисою✅
В. Медіаною
Г. Cтороною

2. Укажіть, який із трикутників госторокутним.
   

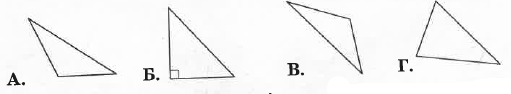
А.
Б.
В.
Г.✅

3. Про ∆ABC i ∆A₁B₁C₁ відомо, що AB = A₁B₁, BC = B₁C₁, AC = A₁C₁, BC = B₁C₁. Тоді...

А. ∆ABC = ∆A₁B₁C₁ (за першою ознакою)
Б. ∆ABC = ∆A₁B₁C₁ (за другою ознакою)
В. ∆ABC = ∆A₁B₁C₁ (за третьою ознакою)✅
Г. рівність трикутників ABC i A₁B₁C₁ установити не можливо

4. Відомо, що ∆PAC = ∆DKF, PC = 5 см, DK = 7 см, KF = 6 см. Знайдіть невідомі сторони ∆PAC i ∆DKF .

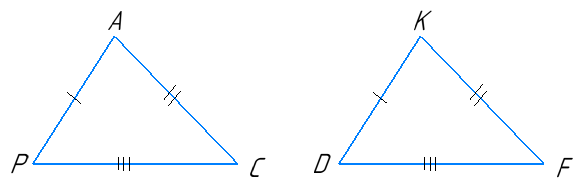
Якщо трикутники рівні, це означає що їх відповідні сторони рівні, тому:
PC = DF = 5 см
AP = DK = 7 см
AC = KF = 6 см

5. Знайдіть периметр рівнобедреного трикутника, бічна сторона якого дорівнює 9 см, а основа на 2 см менша від бічної сторони.

1) 9 – 2 = 7 (см) – довжина основи.
2) P_∆ = 9 + 9 + 7 = 25 (см).

6. На малюнку ∠KAB = ∠LAB, ∠KBA = ∠LBA. Доведіть рівність ∆KAB i ∆LBA.
   

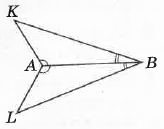
Маємо: два кути одного трикутника рівні двом кутам другого трикутника (∠KAB = ∠LAB, ∠KBA = ∠LBA).
Сторона між цими кутами (AB) спільна.
Отже, ∆KAB = ∆LAB за другою ознакою рівності трикутників.

7. Одна сторона трикутника вдвічі менша від другої і на 2 см менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 34 см.

Нехай сторони трикутника це x, 2x i x + 2
x + 2x + x + 2 = 34
4x = 32
x = 8 см – перша сторона
2 ⋅ 8 = 16 см – друга сторона
8 + 2 = 10 см – третя сторона

8. На малюнку CN = DM, ∠NCD = ∠MDC. Доведіть, що CM = DN.
   
   

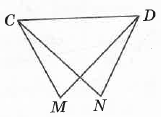
Розглянемо ∆CNM і ∆DMN:
MN - спільна сторона
CN = DM (за умовою)
∠NCM = ∠DMN (за умовою)
За першою ознакою рівності трикутників ∆CNM = ∆DMN, а якщо трикутники рівні, то і всі їх відповідні елементи рівні, тому CM = DN.

9. У рівнобедреному ∆CKL з основою CK проведено медіану LP. Знайдіть периметр трикутника CKL, якщо периметр ∆LPK дорівнює 30 см, а LP = 5 см.

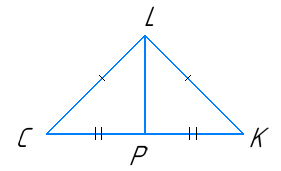
Р_∆LPK = LP + PK + LK;
LK + PK = Р_∆LPK – LP = 30 – 5 = 25 см.
У ∆CKL:
CL = KL (бо трикутник рівнобедрений)
P ділить CK навпіл (бо LP - медіана)
Тоді LC + CP = LK + PK = 25 см.
Р_∆CKL = (LC + CP) + (LK + PK) = 25 + 25 = 50 см.