Діагностична (контрольна) робота ДР-3 [6М] Варіант 2
(Сторінка 33)
- ∆ABC — різносторонній, BK ⊥ до AC. Як називається відрізок BK?
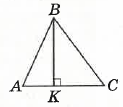
А. Бісектриса трикутника
Б. Медіана трикутника
В. Висота трикутник✅
Г. Cторона трикутника
-
Укажіть, який із трикутників є прямокутним.
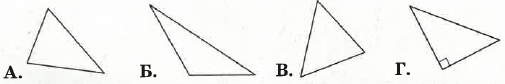
А.
Б.
В.
Г.✅
-
Про ∆ABC i ∆A1B1C1 відомо, що AB = A1B1, BC = B1C1, ∠B = ∠B1. Тоді...
А. ∆ABC = ∆A1B1C1 (за першою ознакою)✅
Б. ∆ABC = ∆A1B1C1 (за другою ознакою)
В. ∆ABC = ∆A1B1C1 (за третьою ознакою)
Г. рівність трикутників ABC i A1B1C1 установити не можливо
-
Відомо, що ∆AKL = ∆PQC, ∠A = 39°, ∠Q = 73°, ∠L = 68°. Знайдіть невідомі кути ∆AKL i ∆PQC.
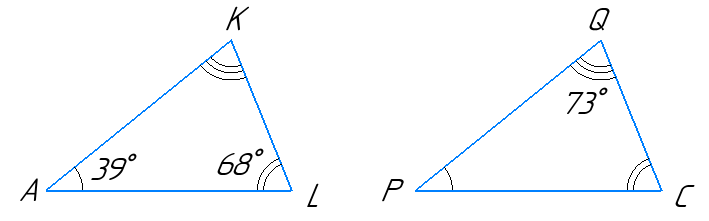
Оскільки ∆AKL та ∆PQC рівні між собою, то їхні відповідні кути рівні:
∠A = ∠P = 39°, ∠K = ∠Q = 73°, ∠L = ∠C = 68°.
- Знайдіть периметр рівнобедреного трикутника, основа якого дорівнює 8 см, а бічна сторона на 2 см більша від основи.
1) 8 + 2 = 10 (см) – довжина бічної сторони
2) P∆ = 10 + 10 + 8 = 28 (см).
-
На малюнку СK = СД, DK = DL. Доведіть рівність ∆CDK i ∆CDL.
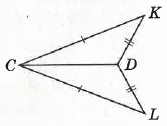
У трикутників CDK і CDL:
CK = CD (за умовою)
DK = DL (за умовою)
CD - спільна сторона
Отже, ∆CDK = ∆CDL за третьою ознакою.
- Одна сторона трикутника на 5 см менша від другої і вдвічі менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 21 см.
Нехай сторони трикутника це x, x + 5 i 2x
x + x + 5 + 2x = 21
4x = 16
x = 4 см – перша сторона
4 + 5 = 9 см – друга сторона
4 ⋅ 2 = 8 см – третя сторона.
- На малюнку ∠CAB = ∠DBA, ∠DAB = ∠CBA. Доведіть, що AC = BD.
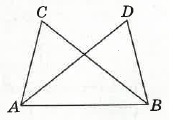
У трикутниках CAB і DBA:
AB - спільна сторона
∠CAB = ∠DBA (за умовою)
∠DAB = ∠CBA (за умовою)
∆CAB = ∆DBA за другою ознакою.
З рівності трикутників випливає рівність відповідних сторін: AC = BD.
- У рівнобедреному ∆MKL з основою MK проведено медіану LA. Знайдіть периметр ∆MKL, якщо периметр ∆LAK дорівнює 24 см, а LA = 8 см.
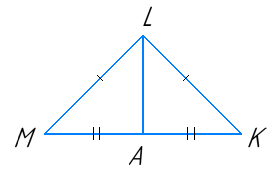
Р∆LAK = LA + AK + LK;
AK + LK = Р∆LAK – LA = 24 – 8 = 16 см.
У ∆MKL: LM = LK (за умовою), MA = AK (оскільки LA – медіана трикутника).
Значить LM + MA = LK + AK = 16 см. Тоді
Р∆MKL = (LM + MK) + (LK + AK) = 16 + 16 = 32 см.
