Діагностична (контрольна) робота ДР-3 [6М] Варіант 1

(Сторінка 32)

1. ∆ABC — різносторонній, ∠ACK = ∠BCK. Як називається відрізок CK?
   
   

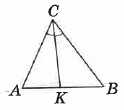
А. сторона трикутника
Б. Бісектриса трикутника✅
В. Висота трикутник
Г. Медіана трикутника

2. Укажіть, який із трикутників є тупокутним.
   

А.
Б.
В.✅
Г.

3. Про трикутники ABC i A₁B₁C₁ відомо, що AC = A₁C₁, ∠A = ∠A₁, ∠С = ∠С₁. Тоді...
   

А. ∆ABC = ∆A₁B₁C₁ (за першою ознакою)
Б. ∆ABC = ∆A₁B₁C₁ (за другою ознакою)✅
В. ∆ABC = ∆A₁B₁C₁ (за третьою ознакою)
Г. рівність трикутників ABC i A₁B₁C₁ установити не можливо

4. Відомо, що ∆MNK = ∆ABC, MN = 5 см, AC = 9 см, BC = 8 см. Знайдіть невідомі сторони ∆MNK i ∆ABC.

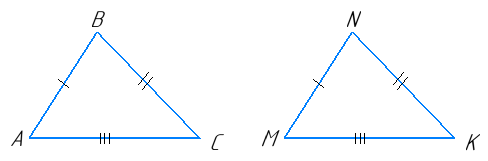
Оскільки у рівних трикутників відповідні сторони рівні, то можемо їх зіставити:
MN = AB = 5 см
NK = BC = 8 см
MK = AC = 9 см.

5. Знайдіть периметр рівнобедреного трикутника, основа якого дорівнює 9 см, а бічна сторона на 2 см менша від основи.

1) 9 – 2 = 7 (см) – довжина бічної сторони

2) P_∆ = 7 + 7 + 9 = 23 (см).

6. На малюнку AM = AN, ∠BAM = ∠BAN. Доведіть рівність ∆AMB i ∆ANB.
   
   

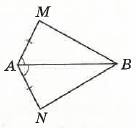
В нас є два трикутники AMB і ANB, які мають: однакові відрізки AM і AN (дано за умовою), спільну сторону AB (бо це одна й та сама сторона для обох трикутників), рівні кути BAM і BAN (дано за умовою).
Якщо у двох трикутників дві сторони і кут між ними рівні, то ці трикутники рівні між собою за першою ознакою. Тому ∆AMB і ∆ANB рівні.

7. Одна сторона трикутника втричі менша від другої і на 6 см менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 31 см.

Нехай сторони трикутника це х, 3x, та x + 6. Тоді:
x + 3x + x + 6 = 31
5x = 25
x = 5 см – перша сторона
3 ⋅ 5 = 15 см – друга сторона
5 + 6 = 11 см – третя сторона

8. На малюнку MK = NL, KN = ML. Доведіть, що ∠NKL = ∠MLK.
   
   

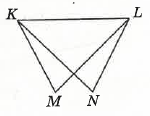
Дивимось на два трикутники ∆MKN і ∆NLM. У них: сторони MK і NL рівні (дано), сторони KN і ML рівні (дано), сторона MN спільна для обох трикутників.
Якщо у двох трикутників всі три сторони рівні, то ці трикутники рівні між собою за третьою ознакою. А якщо трикутники рівні, то й відповідні кути в них рівні. Тому ∠NKL і ∠MLK теж рівні між собою.

9. У рівнобедреному ∆ABC з основою AB проведено медіану CK. Знайдіть периметр ∆ACK, якщо периметр ∆ABC дорівнює 18 см, а CK = 3 см.
   

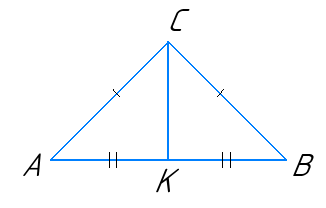
Оскільки AC = BC за умовою, а AK = BK, тому що CK – медіана, то:
AC + AK = BC + BK = P_ABC : 2 = 18 : 2 = 9 см. Тоді:
P_ACK = (AC + AK) + CK  = 9 + 3  = 12 см.