Діагностична (контрольна) робота ДР-3 [6М] Варіант 4
(Сторінка 35)
- ∆ABC — різносторонній, CT ⊥ AB. Тоді відрізок CT є ... трикутника
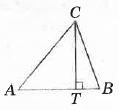
А. Cтороною
Б. Бісектрисою
В. Висотою✅
Г. Медіаною
-
Укажіть, який із трикутників прямокутним.

А.
Б.
В.
Г.✅
-
Про ∆ABC i ∆A1B1C1 відомо, що BC = B1C1, ∠B = ∠B1, ∠C = ∠C1 Тоді...
А. ∆ABC = ∆A1B1C1 (за першою ознакою)
Б. ∆ABC = ∆A1B1C1 (за другою ознакою)✅
В. ∆ABC = ∆A1B1C1 (за третьою ознакою)
Г. рівність трикутників ABC i A1B1C1 установити не можливо
-
Відомо, що ∆MTF = ∆PAB, ∠T = 29°, ∠P = 37°, ∠F = 114°. Знайдіть невідомі кути ∆MTF i ∆PAB.
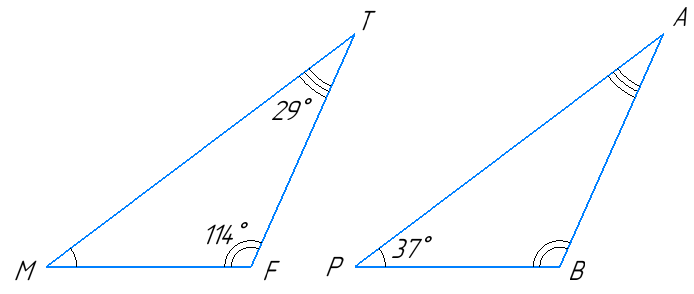
У рівних трикутників відповідні кути рівні, тому:
∠T = ∠P = 29°
∠B = ∠F = 114°
∠M = ∠P = 37°
- Знайдіть периметр рівнобедреного трикутника, бічна сторона якого дорівнює 10 см, а основа на 3 см більша від бічної сторони.
1) 10 + 3 = 13 (см) – довжина основи.
2) P∆ = 10 + 10 + 13 = 33 (см).
-
На малюнку KD = LD, ∠ CDK = ∠ CDL. Доведіть рівність ∆ CDK i ∆CDL.
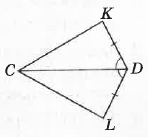
У трикутниках CDK і CDL:
KD = LD (перша пара рівних сторін)
CD - спільна сторона
∠CDK = ∠CDL (пара рівних кутів)
Отже, ∆CDK = ∆CDL за першою ознакою рівності трикутників.
- Одна сторона трикутника на 10 см менша від другої і втричі менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 45 см.
Нехай сторони трикутника це x, x + 10 i 3x
x + x + 10 + 3x = 45
5x = 35
x = 7 см – перша сторона
7 + 10 = 17 см – друга сторона
3 ⋅ 7 = 21 см – третя сторона
- На малюнку AM = BN, MB = NA. Доведіть, що ∠MAB = ∠NBA.
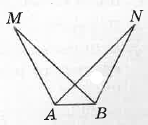
У трикутниках MAB і NBA:
AM = BN (перша пара рівних сторін)
MB = NA (друга пара рівних сторін)
AB = AB (третя пара рівних сторін, як спільна сторона)
Отже, ∆MAB = ∆NBA за третьою ознакою рівності трикутників.
У рівних трикутниках відповідні кути рівні, тому: ∠MAB = ∠NBA
- У рівнобедреному ∆PFK з основою PF проведено медіану KT. Знайдіть периметр трикутника PKT, якщо периметр ∆PFK дорівнює 36 см, а KT = 12 см.
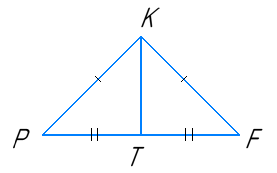
Оскільки PK = KF за умовою, а PT = KT (бо KT медіана), то PK + PT = KF + TF = Р∆PFK : 2 = 36 : 2 = 18 см.
Тоді Р∆PKT = KP + PT + KT = 18 + 12 = 30 см.
