Діагностична (контрольна) робота ДР-2 [4М] Варіант 2

(Сторінка 21)

1. Укажіть малюнок, на якому зображено перпендикулярні прямі.
   
   

А. ✅
Б.
В.
Г. 

2. За малюнком укажіть як називаються кути 1 i 2.
   

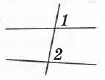
А. Внутрішні односторонні
Б. Вертикальні
В. Відповідні✅
Г. Внутрішні різносторонні

3. На малюнку m i n паралельні, d — січна. Знайдіть градусну міру кута x
   
   

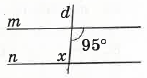
При перетині двох паралельних прямих січною сума внутрішні різносторонні кути рівні, отже х = 95°

А. 85°
Б. 75°
В. 105°
Г. 95°✅

4. Прямі AB, CD i KL перетинаються в точці О. Чи є прямі AB i CD взаємно перпендикулярними якщо
   

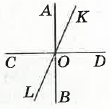
1) ∠AOK = 21°, ∠KOD = 70°

Оскільки:
70° + 21° = 91° ≠ 90°
Прямі AB i CD не є взаємно перпендикулярними

2) ∠DOL = 112°, ∠LOB = 22°

Оскільки:
112° - 22° = 90°
Прямі AB i CD є взаємно перпендикулярними

5. Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 39°. Знайдіть решту кутів

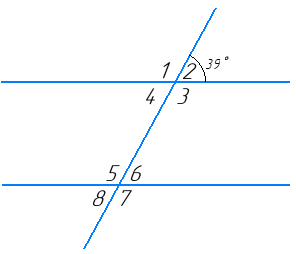
Нехай ∠2 = 39°.
∠4 = ∠2 = 39° (як вертикальні кути).
∠4 = ∠8 = 39° (як відповідні кути).
∠6 = ∠8 = 39° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути).
Звідси ∠1 = 180° – ∠2 = 180° – 39° = 141°.
∠3 = ∠1 = 141° (як вертикальні кути).
∠5 = ∠1 = 141° (як відповідні кути).
∠7 = ∠5 = 141° (як вертикальні кути).

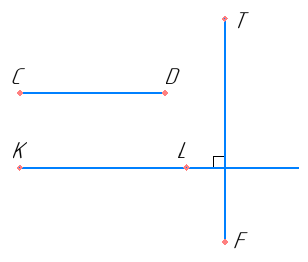
6. Накресліть промені KL та відрізки CD i TF так, щоб промінь KL був паралельний відрізку CD і перпендикулярним до відрізка TF

7. Прямі AB, MN i PK перетинаються в точці O, причому MN перпендикулярний PK. Знайдіть ∠KOB, якщо ∠AOM = 25°
   

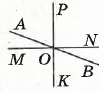
∠AOM = ∠NOB = 25°
∠KOB = ∠NOK - ∠NOB = 90° - 25° = 65°
Відповідь: ∠KOB = 65°.

8. За малюнком знайдіть градусну міру кута x
   
   

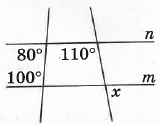
Оскільки сума внутрішніх односторонніх кутів рівна 80° + 100° = 180°, то n ∥ m. Оскільки, при перетині двох паралельних прямих січною відповідні кути рівні, то:
x = 180° - 110° = 70°
Відповідь: x = 70°

9. На малюнку CD ∥ MN. Знайдіть ∠CPM
   
   

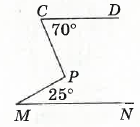
Через т. P проведемо пряму паралельну CD.

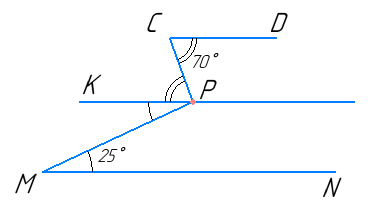
KP ∥ CD, KP ∥ MN. Тоді ∠CPM = ∠CPK + ∠MPK.
Розглянемо MN ∥ KP і січну MP.
∠KPM = ∠PMN = 25° (як внутрішні різносторонні кути).
Розглянемо CD ∥ KP і січну CP.
∠CPK = ∠DCP = 70° (як внутрішні різносторонні кути).
Отже, ∠CPM = 70° + 25° = 95°.
Відповідь: ∠CPM = 95°.