Діагностична (контрольна) робота ДР-5 [9М] Варіант 2

(Сторінка 45)

1. Укажіть запис, що задає функцію:

А. 2a – 7 > 11
Б. y = $\frac{x + 9}{7}$✅
В. 7 + 2x = 2x – 3
Г. 14 : 2 – 6 = 1

2. Укажіть функцію, що є лінійною:

А. y = x² + 5x
Б. y = x² + 5
В. y = 2x + 5✅
Г. y = $\frac{1}{2x + 5}$

3. Лінійну функцію задано формулою y = 9 – 4x. Укажіть коефіцієнт k i l цієї функції:

А. k = –4, l = 9✅
Б. k = 4, l = 9
В. k = 9, l = –4
Г. k = 9, l = 4   

4. Функцію задано формулою y = 2x – 7. Знайдіть:

1) значення функції, якщо значення аргументу дорівнює 5
у = 2 ⋅ 5 – 7 = 10 – 7 = 3

2) значення аргументу, для якого значення функції дорівнює –11
2x – 7 = –11
2x = –4
x = –2 

5. Функцію задано формулою y = 0,4x – 3,6. Не використовуючи побудови:

1) знайдіть нулі функції
0,4x – 3,6 = 0
4x = 36
x = 9

2) з’ясуйте, чи проходить графік функції через точку B(10; 0,6)
0,4 ⋅ 10 – 3,6 = 40 – 3,6 = 36,4 — графік функції не проходить через точку B

6. Побудуйте графік функції y = –3x + 2. Користуючись графіком знайдіть:

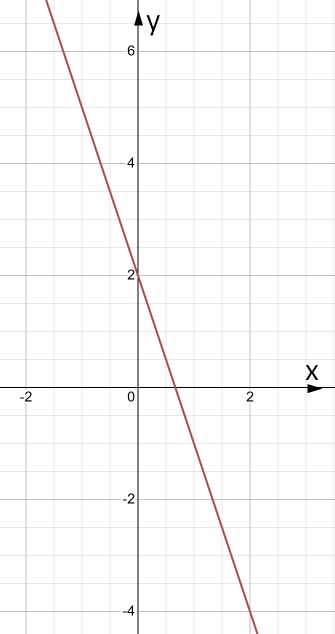
1) значення функції для x = 2
y = –4

2) значення аргументу, для якого y = 5
x = –1

7. Знайдіть область визначення функції y = $\frac{7}{x^2 + 2x}$. 

y = $\frac{7}{x^2 + 2x}$ = $\frac{7}{х(х + 2)}$
Областю визначення функції є множина чисел, крім х = 0 і х = –2.

8. Побудуйте в одній системі координат графіки функції y = 1,5x та y = 3 і знайдіть координати точки перетину:

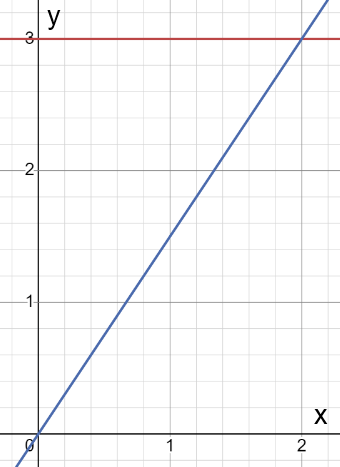
1,5х = 3
х = 2
Функції перетинаються в точці (2; 3)

9. Знайдіть найменше значення функції y = x² – 4x + 3.

Перетворимо функцію у вигляді повного квадрата:
y = x² – 4x + 3 = x² – 4x + 4 – 1 = (х – 2)² – 1
Найменше значення функції y = (х – 2)² – 1 досягається, коли (х – 2)² = 0, тобто х = 2. Тоді:
y = –1
Відповідь: –1.