Завдання № 38

№ 38 ЗПС Геометрія = № 38 ЗПС Математика

Умова:

Два кола мають зовнішній дотик у точці P. Точки M₁ і M₂ — точки дотику спільної зовнішньої дотичної до кіл. Доведіть, що ∠M₁PM₂ = 90°.

Розв'язок:

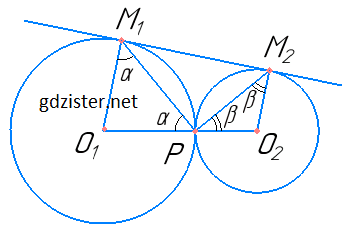
1) Оскільки O₁M₁ ⊥ M₁M₂ і O₂M₂ ⊥ M₁M₂, то O₁M₁ ∥ O₂M₂. Тому AM₁O₁O₂ + AM₂O₂O₁ = 180° (за властивістю внутрішніх різносторонніх кутів).
2) ∆O₁M₁P — рівнобедрений. Позначимо ∠O₁M₁P = ∠O₁PM₂ = α. Тоді α = $\frac{180° – ∠M_{1}O_{1}P}{2}$;
3) ∆O₂M₂P – рівнобедрений. Позначимо ∠O₂M₂P = ∠O₂PM₂ = β. Тоді β = $\frac{180° – ∠M_{2}O_{2}P}{2}$;
4) ∠M₁PM₂ = 180° – (а + β) = 180° – ($\frac{180° – ∠M_{1}O_{1}P }{2}$ + $\frac{180° – ∠M_{2}O_{2}P}{2}$) = 180° – $\frac{360° – (∠M_{1}O_{1}P + ∠M_{2}O_{2}P)}{2}$ = 180° – 180° + $\frac{180°}{2}$ = 90°, що й треба було довести.

Відповідь: