№ 37 ЗПС Геометрія = № 37 ЗПС Математика
Нехай r — радіус кола, вписаного в прямокутний трикутник з катетами a і b та гіпотенузою c. Доведіть, що r = $\frac{(a + b − c)}{2}$
Розв'язок:
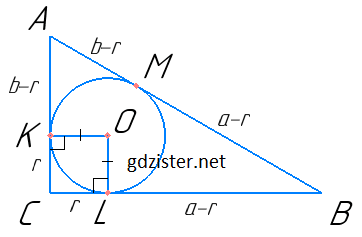
1) Нехай BC = a;
AC = b;
AB = с;
К; L і М — точки дотику.
2) CO — бісектриса кута ACB, тому ∠АСО = $\frac{90°}{2}$ = 45°.
3) У ∆KCO: ∆КОС = 90° – 45° = 45°; ∆KCO — рівнобедрений і CK = OK = r.
4) За властивістю відрізків дотичних, проведених з однієї точки, CL = CK = r.
5) AK = AC – KC = b – r;
BL = BC – CL = а – r.
6) Маємо AM = AK = b – r ;
BM = BL = а – r.
7) AB = AM + MB;
c = b – r + a – r;
2r = a + b – c ;
r = $\frac{a + b – c}{2}$, щo й тpe6a було довести.
