№ 33 ЗПС Геометрія = № 33 ЗПС Математика
Відрізок BD — висота гострокутного трикутника ABC. Від вершини B на прямій BC відкладено відрізки BM і BN, завдовжки як сторона AB. На стороні AC від точки D відкладено відрізок DL, що дорівнює DA. Доведіть, що точки A, M, N, L лежать на одному колі.
Розв'язок:
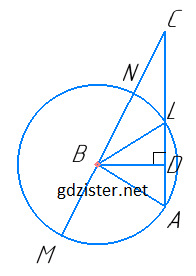
1) Побудуємо коло із центром у точці В і радіусом BA. Зрозуміло, що точки M і N належать цьому колу (оскільки BA = BN = BM).
2) BD є висотою і медіаною ∆BLA, тому ∆BLA — рівнобедрений і BL = BA. Тому точка L також належить побудованому колу.
3) Отже, точки А, М, N і L лежать на одному колі, що й треба було довести.
