№ 31 ЗПС Геометрія = № 31 ЗПС Математика
У трикутнику ABC ∠C = 90°, ∠B = 40°. На сторонах AB і BC позначено точки K і L так, що ∠LAK = 5°, ∠LCK = 10°. Знайдіть ∠LKC.
Розв'язок:
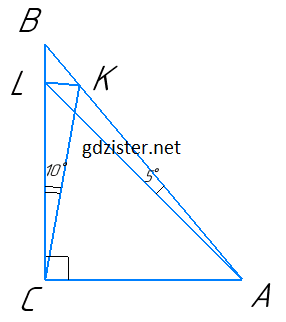
1) ∠BAC = 90° – ∠B = 50°.
2) ∠LAC = 50° – 5° = 45°.
3) ∠KCA = 90° – 10° = 80°.
4) У ∆CKA – ∠CKA = 180° – (80° + 50°) = 50°, тому ∆CKA — рівнобедрений і CK = CA.
5) ∠CLA = 90° – 45° = 45°; тому ∆CLA – рівнобедрений і CL = CA.
6) CK =CA і CL = CA, тому CK = CL; тобто ∆CLK — рівнобедрений і ∠LKC = ∠CLK = $\frac{180° – 10°}{2}$ = 85°.
Відповідь:
85°.
