№ 30 ЗПС Геометрія = № 30 ЗПС Математика
У прямокутному трикутнику один з гострих кутів удвічі менший від другого, а сума гіпотенузи та меншого катета дорівнює a см. Знайдіть радіус кола, описаного навколо трикутника.
Розв'язок:
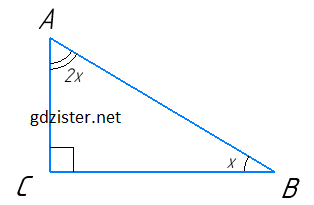
1) Позначимо ∠B = х, тоді ∠A = 2х.
Тоді х + 2х = 90°;
3x = 90°;
x = 30°.
2) Отже, ∠B = 30°, а тому AC = $\frac{AB}{2}$.
3) Позначимо AC = у (см), тоді AB = 2у см.
За умовою у + 2у = а;
3у = а;
у = $\frac{a}{3}$ (см).
4) Оскільки у прямокутному трикутнику радіус описаного кола R дорівнює половині гіпотенузи, то R = $\frac{2y}{2}$ = у = $\frac{a}{3}$ (см).
Відповідь:
$\frac{a}{3}$ см.
