№ 29 ЗПС Геометрія = № 29 ЗПС Математика
Усередині рівностороннього трикутника ABC узято довільну точку K. Доведіть, що AK < BK + KC.
Розв'язок:
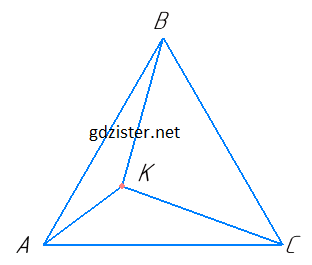
1) ∠KAC < 60°; ∠KCA < 60°, тому ∠AKC > 60° і у ∆AКC кут AKC є найбільший. А отже, AC > AK.
2) У ∆BKC за нерівністю трикутника: BK + KC > BC.
3) Оскільки AC = BC і AC > AK і BK + KC > BC, то AK < BK + KC, що й треба було довести.
