№ 28 ЗПС Геометрія = № 28 ЗПС Математика
У трикутнику ABC AB > AC, AM — медіана. Доведіть, що ∠CAM > ∠MAB.
Розв'язок:
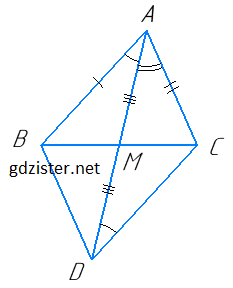
1) Продовжимо медіану AM за точку M на довжину AM, отримаємо точку D.
2) ∠CMD = ∠AMB (як вертикальні). Тому ∆CMD = ∆BMA (за першою ознакою). Тому ∠CDM = ∠MAB i CD = AB.
3) Оскільки AB > АС, то й CD > АС.
4) У ∆CAD: CD > АС, а тому ∠CAD > ∠CDA. Тому ∠CAM > ∠MAB, що й треба було довести.
