№ 26 ЗПС Геометрія = № 26 ЗПС Математика
У трикутнику ABC AC = BC, D — точка перетину бісектрис трикутника, а точка O — центр кола, описаного навколо трикутника. Відрізок OD перетинає сторону AB трикутника в точці P і ділиться цією точкою навпіл. Знайдіть кути трикутника ABC.
Розв'язок:
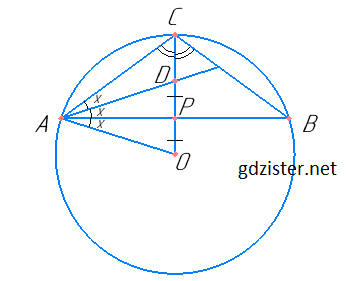
1) Позначимо ∠CAD = ∠DAB = х.
2) CP — серединний перпендикуляр і висота ∆ABC. Тому АР— висота ∆ADO.
3) Оскільки висота ∆ADO є також і медіаною, то AD = AO, а тому AP також і бісектриса ∆ADO. Маємо ∠OAP = х.
4) OA = OC (як радіуси), тому ∠OCA = ∠OAC = 3х.
5) Але в ∆ACP: ∠C = 90° – 2х.
Маємо 3х = 90° – 2х;
5х = 90°;
х = 18°.
6) Отже, ∠CAB = ∠CBA = 2 ∙ 18° = 36°;
∠ACB = 180° – 2 ∙ 36° = 108°.
Відповідь:
36°; 36°; 108°.
