Завдання № 20

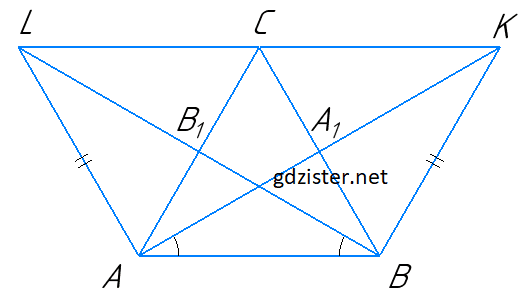
№ 20 ЗПС Геометрія = № 20 ЗПС Математика

ΔABC — рівнобедрений з основою AB. Медіани AA₁ і BB₁ продовжено за точки A₁ і B₁ на відрізки A₁K і B₁L відповідно так, що A₁K = AA₁ і B₁L = BB₁. Доведіть, що ∠ALC = ∠BKC.

Розв'язок:

ΔAB₁B = ΔAA₁B: AB — спільна; AB₁ = BA₁;
∠A = ∠B ⇒ ΔAB₁B = ΔAA₁B ⇒ AA₁ = BB₁, BL = AK.
ΔABL = ΔABK: AB — спільна; BL = AK;
∠A₁AB = ∠B₁BA ⇒ ΔABL = ΔABK; AL = BK.
∠LAB = ∠KBA, ∠LAC = ∠KBC ⇒ ΔALC = ΔBKC.