№ 18 ЗПС Геометрія = № 18 ЗПС Математика
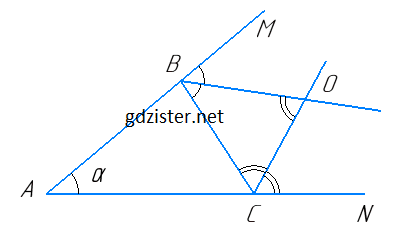
Прямі, що містять бісектриси зовнішніх кутів при вершинах B і C трикутника ABC, перетинаються в точці O. Знайдіть ∠BOC, якщо ∠A = α.
Розв'язок:
∠A + ∠B + ∠C = 180°;
∠B + ∠CBO + ∠MBO = 180° ⇒ ∠CBO = $\frac{α + ∠C }{2}$; ∠C + ∠BCO + ∠OCN = 180°;
∠BCO = $\frac{α + ∠B }{2}$; ∠BOC = 180° –$\frac{α + ∠C }{2}$ – $\frac{α + ∠B }{2}$ = 180° – α – $\frac{∠C + ∠B}{2}$=
= 180° – α – $\frac{180° – α}{2}$ = 180° – α – 90° + $\frac{α}{2}$ = 90° –$\frac{α}{2}$.