№ 807 Геометрія = № 14 ВПТ 10 Математика
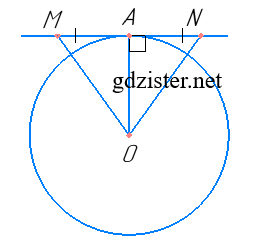
Пряма в точці A дотикається до кола із центром O. На дотичній з різних боків від точки A відкладено рівні відрізки AM і AN. Доведіть, що OM = ON.
Розв'язок:
Нехай MN – дотична до кола, тоді OA ⊥ MN (оскільки дотична до кола є перпендикулярною до радіуса, який проведений в точку дотику).
ΔAOM = ΔAON за двома катетами (OA – спільний катет, AM = AN – за умовою).
Із рівності трикутників випливає, що OM = ON.