№ 802 Геометрія = № 9 ВПТ 10 Математика
У колі через середину радіуса OA перпендикулярно до нього проведено хорду MN. Знайдіть кути трикутника MON.
Розв'язок:
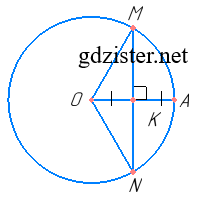
Нехай ОК = АК, MN ⊥ OA.
З ΔOMK: ∠OMK = 30°, оскільки OK = $\frac{1}{2}$ OM.
ΔMON – рівнобедрений, оскільки OM = ON – як радіуси,
тоді ∠ONM = ∠OMN = 30°, ∠MON = 180° – ∠ONM – ∠OMN = 180° – 30° – 30° = 120°.
Отже, в ΔMON ∠MON = 120°, ∠OMN = 30°, ∠MNO = 30°.
Відповідь:
30°, 30°, 120°.
