№ 735 Геометрія = № 50.17 Математика
На малюнку коло вписано в чотирикутник ABCD (дотикається до всіх його сторін). Доведіть, що AB + CD = AD + BC.
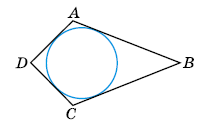
Розв'язок:
Нехай K, L, M, N — точки дотику.
Тоді за властивістю відрізків дотичних, проведених з однієї точки до кола, маємо:
AK = AL, BL = BM, CM = CN, DN = DK.
Додавши почленно чотири останні рівності, маємо:
AK + BM + CM + DK = AL + BL + CN + DN;
(AK + DK) + (BM + CM) = (AL + BL) + (CN + DN); AD + BC = AB + CD.
