Завдання № 732

№ 732 Геометрія = № 50.14 Математика

Умова:

Три кола попарно мають зовнішній дотик. Відрізки, що сполучають їхні центри, утворюють трикутник зі сторонами 5 см, 7 см і 8 см. Знайдіть радіуси цих кіл.

Розв'язок:

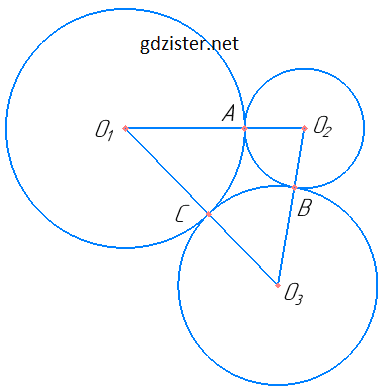
Нехай O₁O₂ = 5 см, O₂O₃ = 7 см, O₁O₂ = 8 см.
Нехай O₁A = r₁, O₂A = r₂, O₂B = r₃,
тоді O₁O₂ + O₂O₃ + O₁O₃ = r₁ + r₂ + r₂ + r₃ + r₃ + r₁ = 2(r₁ + r₂ + r₃).
Тоді r₁ + r₂ + r₃ = $\frac{O_{1}O_{2} + O_{2}O_{3} + O_{1}O_{3}}{2}$ = $\frac{5 + 7 + 8}{2}$ = 10 (см).
r₁ = (r₁ + r₂ + r₃) – O₂O₃ = 10 – 7 = 3 (см);
r₂ = (r₁ + r₂ + r₃) – O₁O₃ = 10 – 8 = 2 (см);
r₃ = (r₁ + r₂ + r₃) – O₁O₂ = 10 – 5 = 5 (см).

Відповідь:

3 см, 2 см, 5 см.