№ 730 Геометрія = № 50.12 Математика
Два кола перетинаються в точках A і B. Точки O1 і O2 — центри цих кіл. Доведіть, що O1O2 ⊥ AB.
Розв'язок:
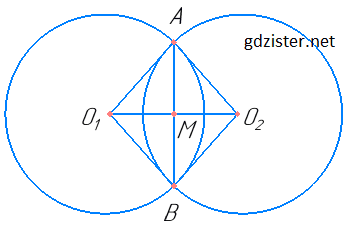
ΔAO1O2 = ΔBO1A2 (за трьома сторонами (O1A = O1B – як радіуси, O2A = O2B – як радіуси, O1O2 – спільна сторона).
З рівності трикутників маємо: ∠AO1O2 = ∠BO1O2.
ΔAO1B – рівнобедрений, оскільки O1A = O1B, O1M – бісектриса, отже, O1M – висота, тобто O1M ⊥ AB, а звідси O1O2 ⊥ AB (так як O1O2 містить O1M).
