№ 710 Геометрія = № 49.15 Математика
Рівнобедрений трикутник ABC вписано в коло із центром у точці O, ∠AOB = 80°. Знайдіть кути трикутника ABC. Скільки розв'язків має задача?
Розв'язок:
Задача має три розв’язки.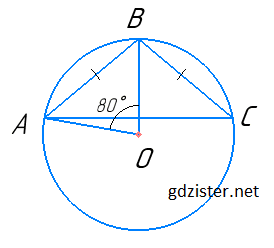
I випадок.
Центральний кут АОВ дорівнює 80°, таку ж градусну міру має дуга, на яку він спирається, а вписаний кут АСВ, що спирається на ту ж дугу, вдвічі менший:
∠АСВ = $\frac{1}{2}$ ∙ 80° = 40°.
∠ВАС = ∠АСВ = 40° як кути при основі.
∠АВС = 180° – (∠АСВ + ∠ВАС) = 180° – (40° + 40°) = 100°.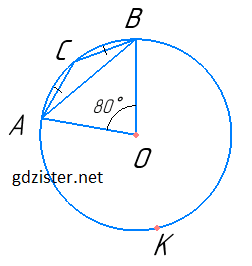
II випадок.
∠АОВ = ◡АСВ = 80° (∠АОВ — центральний), ◡АКВ = 360° – ◡АСВ = 360° – 80° = 280°.
∠АСВ — вписаний.
∠АСВ = $\frac{1}{2}$◡АKВ = 280° : 2 = 140°.
∠CAB = ∠CBA = (180° – ∠АСВ) : 2 = (180° – 140°) : 2 = 20°.
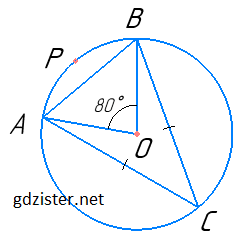
III випадок.
∠АОВ = ◡AРВ = 80°,
∠АСВ = $\frac{1}{2}$◡АРВ = $\frac{1}{2}$ ∙ 80° = 40°.
∠САВ = ∠СВА = (180° – ∠АСВ) : 2 = (180° – 40°) : 2 = 140° : 2 = 70°.
Відповідь:
l - 40°, 40°, 100°.
ll - 140°, 20°, 20°.
lll - 40°, 70°, 70°.
