№ 709 Геометрія = № 49.14 Математика
Доведіть, що кут між дотичною і хордою, що виходить з точки дотику, дорівнює половині дуги, яка лежить між сторонами кута, тобто ∠CAB = $\frac{1}{2}$ ∠CNA.
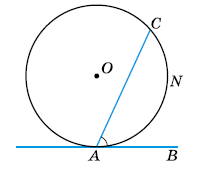
Розв'язок:
Проведемо радіуси ОА і ОС.
∠АОС = ◡СNА (як центральний).
∠ОАС = ∠ОСА = $\frac{180° – ∠АОС}{2}$ = $\frac{180° – ∠CNA}{2}$ = 90° –$\frac{1}{2}$ ◡СNА.
∠ОАВ = 90° як кут між дотичною і радіусом, проведеним в точку дотику.
∠САВ = 90° – ∠ОАС = 90° – (90° –$\frac{1}{2}$◡СNА) = $\frac{1}{2}$◡СNА.
