№ 688 Геометрія = № 48.13 Математика
Доведіть, що радіус кола, описаного навколо рівностороннього трикутника, удвічі більший за радіус кола, вписаного в нього.
Розв'язок:
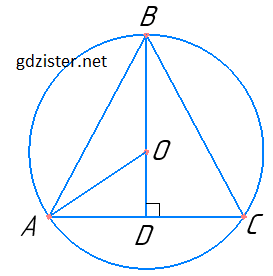
ΔABC – рівносторонній, ∠A = ∠B = ∠C = 60°. Оскільки в рівносторонньому трикутнику медіани перпендикулярні до сторін і одночасно є бісектрисами, то центр вписаного і описаного кола співпадають і лежать на бісектрисі.
∠OAD = $\frac{1}{2}$∠BAD = 60° : 2 = 30°. ΔAOD - прямокутний, тоді AO = 2OD.
OD – радіус вписаного кола, AO – радіус описаного кола. Отже, радіус кола, описаного навколо рівностороннього трикутника, вдвічі більший за радіус кола, вписаного в нього.
