№ 648 Геометрія = № 46.10 Математика
З точки P до кола із центром у точці Q проведено дотичні PM і PN. Доведіть, що промінь PQ — бісектриса кута MPN.
Розв'язок:
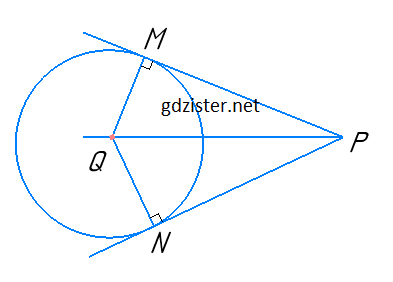
ΔQMP і ΔQNP – прямокутні, оскільки QM ⊥ MP, QN ⊥ NP.
ΔQMP = ΔQNP за двома катетами (QM = QN – як радіуси кола, PM = PN – як відрізки дотичних, проведених з однієї точки до кола).
З рівності трикутників маємо ∠MPQ = ∠NPQ. Отже, PQ – бісектриса кута MPN.
