№ 647 Геометрія = № 46.9 Математика
З точки A до кола із центром у точці O проведено дві дотичні AB і AC (B і C — точки дотику). Доведіть, що промінь OA — бісектриса кута BOC.
Розв'язок:
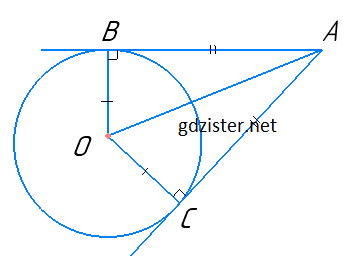
ΔОВА і ΔОСА – прямокутні, оскільки OB ⊥ AB, OC ⊥ AC.
ΔОВА = ΔОСА за двома катетами (OB = OC – як радіуси кола, AB = AC – як відрізки дотичних, проведених з однієї точки до кола).
З рівності трикутників маємо ∠BOA = ∠COA. Отже, ОА – бісектриса кута BOC.
