№ 631 Геометрія = № 45.22 Математика
Доведіть, що коли хорди рівновідда лені від центра кола, то вони між собою рівні.
Розв'язок:
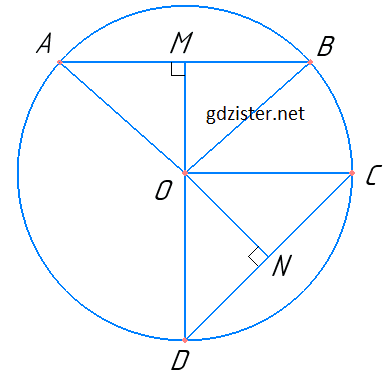
Нехай AB і CD – хорди. OM ⊥ AB, ON ⊥ CD і OM = ON. Доведемо, що AB = CD.
Оскільки OM ⊥ AB; ON ⊥ CD, то AM = MB, DN = CD, тобто, щоб довести,
що AB = CD, досить довести, що AM = CN.
ΔAOM = ΔCON (за гіпотенузою і катетом: OM = ON – за умовою, OA = OC – як радіуси кола), тоді AM = CN.
Отже, AB = 2AM = 2CN = CD.
