№ 604 Геометрія = № 29 ВПТ 8 Математика
Доведіть, що в нерівнобедреному прямокутному трикутнику бісектриса прямого кута ділить кут між висотою і медіаною, проведеними з тієї самої вершини, навпіл.
Розв'язок:
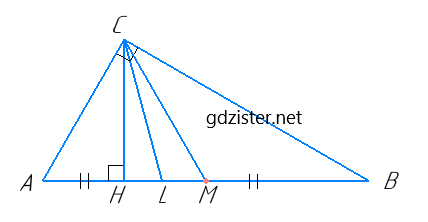
Нехай у прямокутному трикутнику ABC (∠C = 90°), CH – висота, CL – бісектриса, CM – медіана, ∠HCL = β. Доведемо, що ∠LCM = β.
Оскільки CL – бісектриса, то ∠ACL = ∠LCB = 90° : 2 = 45°, тоді ∠ACH = ∠ACL – ∠HCL = 45° – β.
З прямокутного ΔACH: ∠A = 90° – ∠ACH = 90° – (45° – β) = 45° + β.
З прямокутного ΔABC: ∠B = 90° – ∠A = 90° – (45° + β) = 45° – β.
ΔCMB – рівнобедрений, оскільки CM = MB (за властивістю медіани, проведеної до гіпотенузи), тоді ∠MCB = ∠B = 45° – β.
Отже, ∠LCM = ∠LCB – ∠MCB = 45° – (45° – β) = 45° – 45° + β = β.
Отже, бісектриса прямого кута ділить кут між висотою і медіаною, проведеними з вершини прямого кута, навпіл.
