№ 603 Геометрія = № 28 ВПТ 8 Математика
Медіана, проведена до гіпотенузи прямокутного трикутника, дорівнює 10 см і ділить прямий кут у відношенні 1:2. Знайдіть гіпотенузу та менший катет трикутника.
Розв'язок:
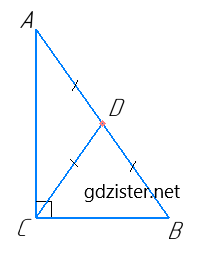
Нехай в прямокутному ΔABC CD – медіана, CD = 10 см, ∠ACD : ∠DCB = 1 : 2, отже, ∠ACD = 90° : 3 = 30°, ∠DCB = (90° : 3) · 2 = 60°.
Оскільки медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи, то AB = 2CD = 2 · 10 = 20 см, CD = DB, CD = AD. Отже, ΔCDB – рівнобедрений, оскільки ∠DCB = ∠DBC = 60°. Оскільки сума кутів трикутника дорівнює 180°, то ∠CDB = 180° – (∠DCB + ∠DBC) = 180° – 120° = 60°. Отже, ΔCDB – рівносторонній, CB = CD = DB = 10 см.
Відповідь:
20 см, 10 см.
