№ 600 Геометрія = № 25 ВПТ 8 Математика
Знайдіть кут між бісектрисами гострих кутів прямокутного трикутника.
Розв'язок:
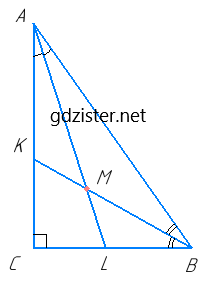
Нехай в прямокутному ΔABC (∠C = 90°), ∠A = α, ∠B = β, α + β = 90°.
∠MAB = $\frac{∠A }{2}$ = $\frac{α}{2}$, ∠MBA = $\frac{∠B }{2}$ = $\frac{β}{2}$, тоді ∠AMB = 180° – ∠MAB – ∠MBA = 180° – $\frac{α}{2}$ – $\frac{β}{2}$ = 180° – $\frac{1}{2}$(α + β) = 180° – $\frac{1}{2}$ · 90° = 180° – 45° = 135°.
∠LMB – суміжний з кутом AMB. ∠LMB = 180° – 135° = 45°.
Відповідь:
45°.
