№ 598 Геометрія = № 23 ВПТ 8 Математика
З вершини прямого кута прямокутного трикутника проведено бісектрису і висоту, кут між якими 15°. Знайдіть гострі кути трикутника.
Розв'язок:
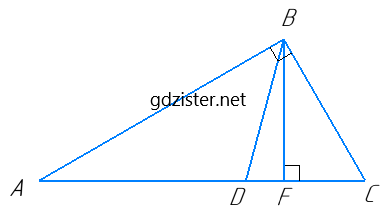
Нехай у прямокутному ΔABC (∠B = 90°), BF ⊥ AC,
∠ABD = ∠DBC = 90° : 2 = 45°, ∠DBF = 15°. ∠FBC = ∠DBC – ∠DBF = 45° – 15° = 30°.
З прямокутного трикутника BCF: ∠BCF = 90° – ∠FBC = 90° – 30° = 60°.
З прямокутного ΔABC: ∠A = 90° – ∠C = 90° – 60° = 30°,
оскільки сума гострих кутів трикутника дорівнює 90°.
Відповідь:
60°, 30°.
