№ 593 Геометрія = № 18 ВПТ 8 Математика
Внутрішній кут трикутника дорівнює різниці зовнішніх кутів, не суміжних з ним. Доведіть, що трикутник — прямокутний.
Розв'язок:
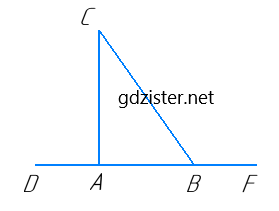
Нехай ∠CBF = ∠CAD = ∠C.
∠CBF = 180° – ∠CBA, ∠CAD = 180° – ∠CAB,
тоді ∠C = ∠CBF – ∠CAD = 180° – ∠CBA – 180° + ∠CAB = ∠CAB – ∠CBA.
Звідси ∠CAB = ∠C + ∠CBA. ∠C + ∠CAB + ∠CBA = 180° (за теоремою про суму кутів трикутника). Оскільки ∠C + ∠CBA = ∠CAB, маємо ∠CAB + ∠CAB = 180°,
2∠CAB = 180°, ∠CAB = 90°. Отже, ΔABC – прямокутний.
