№ 591 Геометрія = № 16 ВПТ 8 Математика
Сума внутрішніх кутів рівнобедреного трикутника разом з одним із зовнішніх кутів дорівнює 260°. Знайдіть градусні міри внутрішніх кутів трикутника.
Розв'язок:
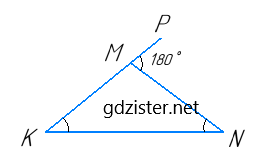
Оскільки сума внутрішніх кутів трикутника дорівнює 180°, то зовнішній кут трикутника дорівнює 260° – 180° – 80°. Цей зовнішній кут не може бути при основі трикутника, оскільки в такому випадку кути при основі дорівнюватимуть 180° – 80° = 100°, це неможливо.
Нехай в ΔKMN ∠PMN = 80°, тоді ∠KMN = 180° – 80° = 100° (оскільки ∠KMN і ∠PMN суміжні). ∠K = ∠N, оскільки трикутник KMN – рівнобедрений. За властивістю зовнішнього кута трикутника маємо ∠K+∠L = ∠PMN, ∠K = ∠L = $\frac{1}{2}$∠PMN = $\frac{1}{2}$ · 80° = 40°.
Відповідь:
100°, 40°, 40°.
