№ 589 Геометрія = № 14 ВПТ 8 Математика
Один з кутів трикутника дорівнює половині зовнішнього кута, не суміжного з ним. Доведіть, що трикутник — рівнобедрений.
Розв'язок:
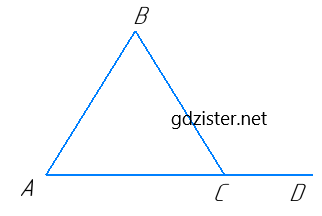
Нехай ∠A = $\frac{1}{2}$∠BCD, тоді оскільки зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним, ∠B = $\frac{1}{2}$∠BCD. Таким чином, ∠A = ∠B, отже, згідно з означенням рівнобедреного трикутника, ΔABC – рівнобедрений.
