№ 582 Геометрія = № 7 ВПТ 8 Математика
Бісектриса одного з кутів трикутника утворює з висотою, проведеною з тієї самої вершини, кут 16°, а менший з двох інших кутів трикутника дорівнює 50°. Знайдіть невідомі кути трикутника.
Розв'язок:
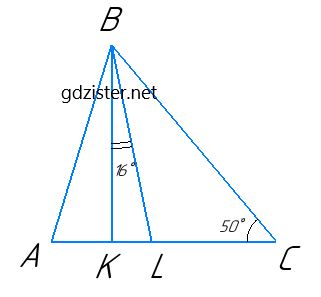
Нехай в ΔABC: BL — бісектриса, BK — висота, BK ⊥ AC, ∠KBL = 16°, ∠BCA = 50°. З ΔBKL: ∠BLK = 180° – ∠BKL – ∠KBL = 180° – 90° – 16° = 74°.
∠BLC + ∠BLK = 180° як суміжні кути, звідси ∠BLC = 180° – ∠BLK = 180° – 74° = 106°.
З ΔBLC: ∠LBC = 180° – ∠BLC – ∠C = 180° – 106° – 50° = 24°.
Оскільки BL – бісектриса, то ∠ABC = 2 · 24° = 48°.
З ΔABC: ∠A = 180° – ∠ABC – ∠C = 180° – 48° – 50° = 82°.
Відповідь:
48°, 82°.
