№ 581 Геометрія = № 6 ВПТ 8 Математика
Знайдіть кут між двома прямими, що містять медіани рівностороннього трикутника.
Розв'язок:
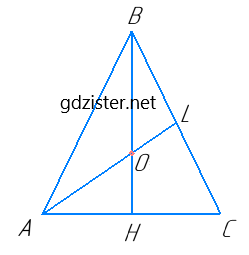
Нехай ΔABC – рівносторонній, AB = BC = AC, AL, BH – медіани, AH = HC, BL = LC.
Оскільки ΔABC – рівносторонній, то ∠A = ∠B = ∠C = 60°. Оскільки AL і BH – медіани рівностороннього трикутника, то вони є бісектрисами і висотами, тоді ∠LAH = 60° : 2 = 30°, ∠BHA = 90°.
З ΔAOH : ∠AOH = 180° – ∠OAH – ∠OHA = 180° – 30° – 90° = 60°.
Відповідь:
60°.
