№ 571 Геометрія = № 28 ВПТ 6 Математика
На малюнку ∠ABD = ∠ADB, ∠CBD = ∠CDB. Доведіть, що BD ⊥ AC.
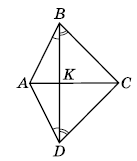
Розв'язок:
Оскільки ∠ABD = ∠ADB, то ΔABD – рівнобедрений згідно з ознакою рівнобедреного трикутника, тоді AB = AD.
Оскільки ∠DBC = ∠CDB, то ΔBCD – рівнобедрений згідно з ознакою рівнобедреного трикутника, тоді CB = CD.
ΔABC = ΔADC за двома сторонами і кутом між ними
(AB = AD, BC = DC – за доведенням, ∠B = ∠D – як сума рівних кутів).
Із рівності цих трикутників маємо ∠BCA = ∠DCA.
Оскільки пряма AC містить бісектрису кута C рівнобедреного трикутника BCD, то пряма AC містить висоту ΔBCD. Отже, AC⊥BD.
