Завдання № 569

№ 569 Геометрія = № 26 ВПТ 6 Математика

AM і A₁M₁ — відповідно медіани рівних між собою трикутників ABC і A₁B₁C₁. Доведіть, що ∆ABM = ∆A₁B₁M₁.

Розв'язок:

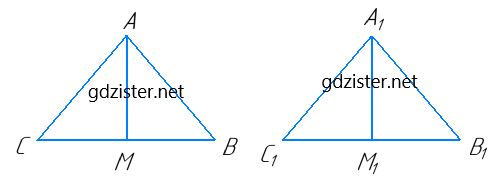
Нехай ΔABC = ΔA₁B₁C₁, AM – медіана ΔABC (CM = MB),
A₁M₁ – медіана ΔA₁B₁C₁ (C₁M₁ = M₁B₁).
Розглянемо ΔABM і ΔA₁B₁M₁: AB = A₁B₁ – як відповідні сторони рівних трикутників, ∠B = ∠B₁ – як відповідні кути рівних трикутників. MB = M₁B₁ – як половини рівних сторін. Отже, ΔABM = ΔA₁B₁M₁ за першою ознакою рівності трикутників.