ДСР 3 Геометрія = ДСР 6 Математика
АВ - основа рівнобедреного трикутника АВС, СК його бісектриса. Знайдіть довжину цієї бісектриси, якщо периметр трикутника АВС дорівнює 36 см, а периметр трикутника АСК дорівнює 30 см.
А. 6 см
Б. 8 см
В. 10 см
Г. 12 см
Розв'язок:
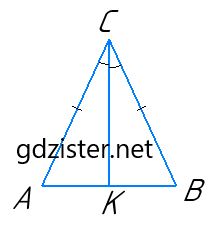
Оскільки CK — бісектриса рівнобедреного трикутник, що проведена до основи, то CK є також і медіаною. Отже, AK = KB.
За умовою AC = CB.
P∆ABC = AC + AB + CB = 2АС + 2AK = 2(AC + AK). Тому AC + AK = $\frac{36}{2}$ = 18 (см).
P∆AСК = AC + AK + CK. Тому CK = 30 – 18 = 12 (см).
Відповідь:
Г) 12 см.
