Завдання № 520

№ 520 Геометрія = № 40.27 Математика

Умова:

Доведіть, що коли медіана трикутника ділить його на два трикутники з однаковими периметрами, то хоча б два кути трикутника між собою рівні.

Розв'язок:

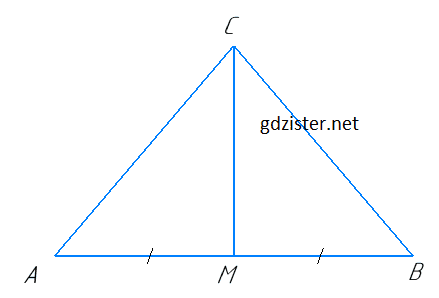
Нехай CM - медіана, P_ΔACM = P_ΔCMB. Оскільки P_ΔACM = AC + CM + AM,
P_ΔCMB = BC + CM + MB і ці периметри рівні, то AC + CM + AM = BC + CM + MB.
Звідси AC + AM = BC + MB. Враховуючи, що AM = MB, матимемо AC = BC.
Отже, у трикутника ABC хоча б дві сторони рівні, а отже, рівні і хоча б два кути.

Відповідь: