№ 518 Геометрія = № 40.25 Математика
Різниця градусних мір двох зовнішніх кутів при вершинах гострих кутів прямокутного трикутника дорівнює 20°. Знайдіть гострі кути трикутника.
Розв'язок:
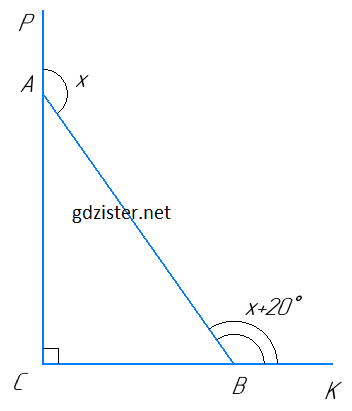
Нехай у прямокутному трикутнику ABC (∠C = 90°), ∠PAB і ∠ABK - зовнішні кути при вершинах гострих кутів.
Нехай ∠PAB = x°, тоді ∠ABK = x° + 20°.
∠CAB + ∠PAB = 180° (як суміжні кути), звідси ∠CAB = 180° – ∠PAB = 180° – x°. ∠ABC + ∠ABK = 180° (як суміжні кути), звідси ∠ABC = 180° – ∠ABK = 180° – (x° + 20°) = 160° – x°.
Оскільки сума гострих кутів прямокутного трикутника дорівнює 90°, маємо рівняння: 180° – х + 160° - х = 90°; 2x = 250°; x = 125°.
Отже, ∠CAB = 180° – 125° = 55°, ∠ABC = 160 - 125° = 35°.
Відповідь:
55°, 35°.
