№ 516 Геометрія = № 40.23 Математика
У прямокутному трикутнику один з кутів дорівнює 60°, а сума гіпотенузи і меншого катета — 30 см. Знайдіть довжину гіпотенузи та медіани, що проведена до неї.
Розв'язок:
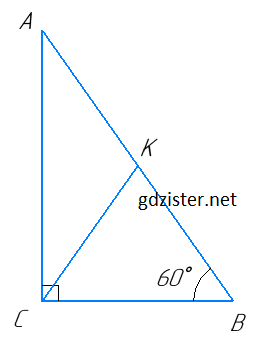
Нехай ΔABC — прямокутний (∠C = 90°),
∠B = 60°, AB + CB = 30 см, СК — медіана. ∠A = 90° - 60° = 30° (оскільки сума гострих кутів прямокутного трикутника дорівнює 90°). Нехай BC = x, тоді AB = 2x (оскільки катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи).
Складемо рівняння: x + 2x = 30; 3x = 30; x = 10, тоді 2x = 2 × 10 = 20. Отже, AB = 20 см. Оскільки СК — медіана, проведена до гіпотенузи, то CK = $\frac{1}{2}$AB = $\frac{1}{2}$ × 20 = 10 (см).
Відповідь:
20 см, 10 см.
