№ 512 Геометрія = № 40.19 Математика
Доведіть, що точка, яка лежить у внутрішній області кута і рівновіддалена від його сторін, належить бісектрисі цього кута.
Розв'язок:
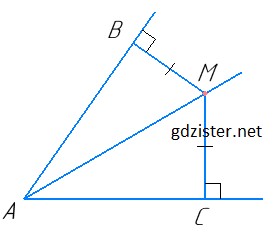
Нехай т. М розміщена всередині кута BAC, MB ⊥ AB, MC ⊥ AC, BM = CM. Доведемо, що точка М належить бісектрисі кута A, тобто ∠BAM = ∠CAM.
ΔABM = ΔACM за гіпотенузою і катетом (AM — спільна гіпотенуза, BM = CM), тоді ∠BAM = ∠CAM.
