№ 511 Геометрія = № 40.18 Математика
Знайдіть більший з кутів, що утворює бісектриса прямого кута трикутника з гіпотенузою, якщо один з гострих кутів трикутника дорівнює 68°.
Розв'язок:
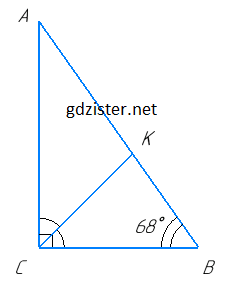
Нехай в прямокутному ΔABC (∠C = 90°) CK — бісектриса.
∠ACK = ∠KCB = 90° : 2 = 45°.
З ΔCKB ∠CKB = 180° – (∠KCB + ∠B) = 180° – (45° + 68°) = 67° (за теоремою про суму кутів трикутника).
Тоді ∠CKA = 180° – ∠CKB = 180° – 67° = 113°.
Отже, більший кут між бісектрисою прямого кута і гіпотенузою дорівнює 113°.
Відповідь:
113°.
