№ 509 Геометрія = № 40.16 Математика
Знайдіть гострі кути прямокутного трикутника, якщо:
1) один з них у 4 рази більший за другий;
2) один з них на 16° менший від другого;
3) їхні градусні міри відносяться як 5:4.
Розв'язок:
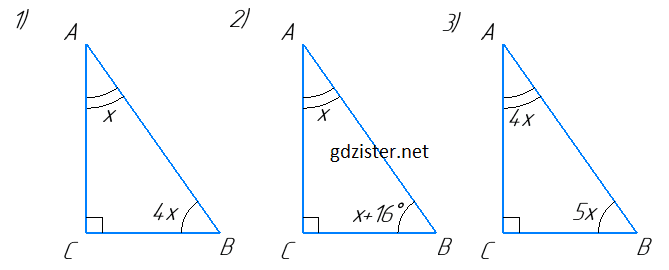
1) Нехай в прямокутному ΔABC ∠A = x°, ∠B = 4x°.
Оскільки в прямокутному трикутнику сума гострих кутів дорівнює 90°, то маємо:
x + 4x = 90°; 5x = 90°; x = 18°.
Отже, ∠A = 18°, ∠B = 18° × 4 = 72°.
2) Нехай в прямокутному ΔABC ∠A = x, тоді ∠B = x + 16°.
Оскільки в прямокутному трикутнику сума гострих кутів дорівнює 90°, то маємо:
x + x + 16° = 90°; 2x = 74°; x = 37°.
Отже, ∠A = 37°, ∠B = 37° + 16° = 53°.
3) Нехай в прямокутному ΔABC ∠B = 5x, ∠A = 4x.
Оскільки сума гострих кутів прямокутного трикутника дорівнює 90°, то маємо:
5x + 4x = 90°; 9x = 90°; x = 10°.
Отже, ∠B = 5 × 10° = 50°, ∠A = 4 × 10° = 40°.
Відповідь:
1) 18°, 72°.
2) 37°, 53°.
3) 50°, 40°.
