№ 487 Геометрія = № 39.25 Математика
Доведіть, що бісектриси зовнішнього і внутрішнього кутів трикутника при одній вершині перпендикулярні між собою.
Розв'язок:
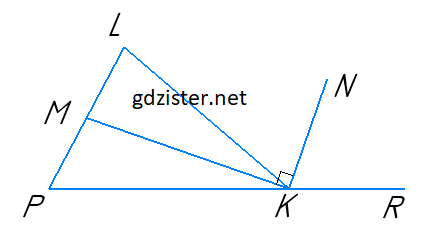
Нехай ΔPLK — даний трикутник. ∠PKL і ∠LKR — суміжні. KM — бісектриса кута LKP. ∠PKM = ∠LKM. KN — бісектриса ∠LKR, ∠LKN = ∠NKR. ∠PKL + ∠LKR = 180°,
∠PKM + ∠LKM + ∠LKN + ∠NKR = 180°,
2∠LKM + 2∠LKN = 180°, 2(∠LKM + ∠LKN) = 180°,
∠LKM + ∠LKN = 90°. Отже, KM ⊥ KN.
